fusione e stereopsi

Vogliamo chiarirci se il fenomeno della fusione e il fenomeno della stereopsi, della visione binoculare, sono legati o meno, cioè se dove c’è fusione c’è steropsi e viceversa. A tal fine costruiamo la prospettiva di un pavimento a scacchiera come è visto da un occhio, ponendo il punto di vergenza al centro della stanza: per rendere ciò evidente nella prospettiva facciamo un asse verticale, il cui limite inferiore rappresenta il suddetto punto. Fatto ciò facciamo un flip orizzontale per ricavare una prospettiva simmetrica a questa. Affianchiamo le due prospettive per ricavare un’autostereografia. Chi ha difficoltà in questo senso può sempre ricorrere allo stereoscopio. Vedere il disegno seguente:

L’immagine binoculare che si ricava, non tenendo conto della stereopsi, è la seguente:

L’immagine è pulita perché la fusione orizzontale ha fuso le rette oblique che rappresentano la profondità, però possiamo notare che c’è stata anche una fusione verticale per le rette che rappresentano la larghezza. Questa fusione che riguarda la disparità verticale non produce stereopsi, come si può notare nel disegno seguente che riproduce la condizione di prima senza le rette della profondità:

Nella visione stereografica dell’immagine sopra, la fusione avviene, ciò che manca è la stereopsi. Le stesse rette, messe in verticale e viste in autostereografia, producono stereopsi, come si può constatare dall’immagine sotto:

Dalle suddette esperienze possiamo concludere che la fusione è presente sia nella disparità orizzontale, ed in tal caso è combinata con la stereopsi, sia nella disparità verticale, ed in tal caso è uno dei tanti strumenti della mente per pulire la sovrapposizione delle immagini retiniche. Invece la stereopsi è legata al sistema punto di vergenza-disparità orizzontale.

sul significato della parola arte 2

Baumgarten divideva la conoscenza in estetica e logica, attribuiva all’estetica una conoscenza confusa, mentre attribuiva alla logica una conoscenza distinta. L’arte era per lui una conoscenza confusa, infatti i libri che parlano di arte sono pieni di termini che non hanno nessun significato. In questi l’arte è “quel qualche cosa”, che non è possibile definire meglio. Questo non solo ai tempi di Baumgarten, ancora è così: per esempio io ho studiato sul Salvini, sto parlando del 1967, il quale finiva sempre la descrizione delle opere dicendo che avevano un “quid” che distingueva ciò che era arte da ciò che non lo era. Ciò perché l’arte non è opera di un uomo, ma di un semidio chiamato genio. E l’uomo può definire con il linguaggio l’opera di un quasi Dio? Scriveva Edward Young nel 1759: “Siamo grati al sapere ma riveriamo il genio; il primo ci dà piacere, il secondo ci rapisce; quello ci informa, questo ci ispira… il genio infatti deriva dal cielo, il sapere dall’uomo”. Lo scopo di questo lavoro è capire da dove viene il concetto di artista genio, se questo ci serve per parlare di arte è bene continuare ad usarlo, ma se è solo frutto di fantasia perché mantenere ancora nell’arte un linguaggio così ambiguo?

Prima del quattrocento, stiamo parlando dell’umanesimo, due erano le necessità dell’uomo: quella del fare, affidata ai tecnici, e quella del teorizzare, affidata agli scienziati. A noi non interessa se il lavoro dello scienziato veniva posto più in alto del lavoro del tecnico, ciò che a noi interessa è che in questo periodo si ricorre ad una terza figura, l’artista, in grado di soddisfare i bisogni più alti dell’uomo, quelli spirituali. Tutto ciò nacque nella Firenze quattrocentesca, da un interesse per la storia patria. In questo periodo si cominciò a scrivere della vita dei pittori, scultori ed architetti che con le loro opere davano lustro alla città, presentandoli come eroi, come eredi della tradizione greca e romana. Per esempio Botticelli fu chiamato il nuovo Apelle. In questo periodo furono ritrovati e pubblicati diversi testi antichi, Vitruvio, Cicerone, Plinio, che davano sicurezza a questo aggancio alla tradizione, anzi era un modo per dare importanza agli artisti fiorentini. Tutta questa ricerca si svolgeva all’interno di una cornice neoplatonica, ecco perché ai pittori, scultori e architetti furono attribuite qualità che erano legate ai miti della filosofia di Platone, soprattutto dobbiamo riferirci alle opere del Timeo (nel quale l’anima del mondo, precipitata sulla Terra dall’Iperuranio, riacquista le ali grazie a Eros, e può tornare a contemplare la perfezione delle idee), e del Simposio, dove Amore è, per natura, a metà tra ignoranza e sapienza. Riporto un poco del Simposio a maggior chiarimento:

- Quando nacque Afrodite gli dei tennero un banchetto, e fra gli altri anche Poro (Espediente) figlio di Metidea (Sagacia). Ora quando ebbero finito, arrivò Penia (Povertà), siccome era stata gran festa, per mendicare qualcosa; e si teneva vicino alla porta. Poro intanto, ubriaco di nettare, inoltrandosi nel giardino di Giove, schiantato dal bere si addormentò. Allora Penia meditando se, contro le sue miserie, le riuscisse avere un figlio da Poro, gli si sdraiò accanto e rimase incinta di Amore. Proprio così Amore divenne seguace e compagno di Afrodite, perché fu concepito il giorno della sua nascita, ed ecco perché di natura è amante del bello, in quanto anche Afrodite è bella. Dunque, come figlio di Poro e Penia, ad Amore è capitato questo destino: innanzitutto è sempre povero, ed è molto lontano dall'essere delicato e bello, come pensano in molti, ma anzi è duro, squallido, scalzo, peregrino, uso a dormire nudo e frusto per terra, sulle soglie delle case e per le strade, le notti all'addiaccio; perché conforme alla natura della madre, ha sempre la miseria in casa. Ma da parte del padre è insidiatore dei belli e dei nobili, coraggioso, audace e risoluto, cacciatore tremendo, sempre a escogitar intrighi d'ogni tipo e curiosissimo di intendere, ricco di trappole, intento tutta la vita a filosofare, e terribile ciurmatore, stregone e sofista. E sortì una natura né immortale né mortale, ma a volte, se gli va dritta, fiorisce e vive nello stesso giorno, a volte muore e poi risuscita, grazie alla natura del padre; ciò che acquista sempre gli scorre via dalle mani, così Amore non è mai né povero né ricco. Anche tra sapienza ed ignoranza si trova a mezza strada, e per questa ragione nessuno degli dei è filosofo, o desidera diventare sapiente (che lo è già), né chi è già sapiente s'applica alla filosofia. D'altra parte, neppure gli ignoranti si danno a filosofare né aspirano a diventare saggi, ché proprio per questo l'ignoranza è terribile, che chi non è né nobile né saggio crede d'aver tutto a sufficienza; e naturalmente chi non avverte di essere in difetto non aspira a ciò di cui non crede d'aver bisogno.//. Poiché appunto la sapienza lo è delle cose più belle ed Amore è amore del bello, ne consegue necessariamente che Amore è filosofo, e in quanto tale sta in mezzo fra il sapiente e l'ignorante. Anche di questo la causa è nella sua nascita: è di padre sapiente e ingegnoso, ma la madre è incolta e sprovveduta-.

Nel racconto di Platone Amore ha tutte le caratteristiche del genio. Infatti il genio è ignorante perché non ha studiato, ma nello stesso tempo possiede la sapienza perché fa le cose giuste. Come Amore è la terza posizione su tutto, tra mortalità e immortalità, tra ricchezza e povertà, così il genio è la terza posizione su tutto, anche tra il fare e il pensare, tra il tecnico e lo scienziato. Così nacque, nella Firenze rinascimentale, dopo il tecnico e lo scienziato, la terza figura: l’artista. Il concetto di artista ci parla dell’ammirazione che riescono a suscitare alcuni uomini in noi tutti, ma non dice niente dell’arte. Il linguaggio confuso di cui ci serviamo per descrivere questa figura, metà uomo e metà Dio, è un fatto filosofico e critico, non artistico.

La diplopia e la visione binoculare dello spazio

Nel 1972 il Dr. Bela Julesz presentò gli RDS, o Random Dot Stereograms, dimostrando che la visione della profondità è fondata sul sistema convergenza-disparità. Si tratta di una coppia di disegni che se guardati in diplopia, cioè guardando oltre i due disegni fino a vederne tre, l'immagine di mezzo, essendo la combinazione delle due, è stereografica e mostra il rilievo.

Gli oggetti che si trovano nell'area di Panum vengono fusi e visti in tre dimensioni. La fusione è la deformazione delle due immagini da parte del cervello per farle combaciare. Ciò è messo in evidenza dal seguente disegno stereografico, che a tal fine usa colori diversi.

Nella stereografia si ha, partendo da sinistra verso destra: la prima immagine è la nera; la seconda è la combinazione della nera con la rossa; la terza è la combinazione della rossa con la verde; la quarta è la verde. Dato che si vengono a sovrapporre disegni diversi, dato che i due disegni combaciano, vuol dire che c'è stato un adattamento operato dal cervello.

Ciò che sta fuori dall'area di Panum viene visto in diplopia ed è ciò che si vuole indagare con il presente lavoro al fine di chiarire il ruolo della diplopia nella visione della profondità. Esistono due tipi di diplopia: la diplopia omonima riguarda gli oggetti che sono oltre l'area di Panum, riguarda gli oggetti che si trovano più lontano del punto di vergenza; invece la diplopia crociata si riferisce agli oggetti più vicini rispetto al punto di vergenza e si chiama così perché l'immagine di destra è vista dall'occhio sinistro e viceversa, cioè c'è un incrocio dei raggi visuali.

Facciamo un disegno in cui disponiamo una griglia ortogonale di punti equamente distanziati, sia in verticale come in orizzontale, composta da 25 colonne e da 15 righe:

Poi disegniamo dei quadratini di tre colori come il seguente disegno:

Guardando il disegno in stereografia, quando guadiamo i quadratini azzurri vediamo quelli verdi e neri in diplopia crociata, in quanto più vicini del punto di vergenza; al contrario guardando i quadratini neri vediamo quelli verdi e azzurri in diplopia omonima perché più lontani del punto di vergenza. Dobbiamo vedere se, in relazione alla percezione della profondità, c'è differenza tra quella omonima e crociata. Iniziamo da quella crociata soffermandoci sui quadratini azzurri. Muovendo lo sguardo, saltando sempre negli azzurri, ci accorgiamo, non cambiando piano di vergenza, che delle linee immaginarie in profondità uniscono i quadratini neri, verdi e azzurri, come in una prospettiva.

Questo significa che la diplopia crociata genera stereopsi di primo livello, crea uno spazio in cui gli oggetti hanno una collocazione precisa nella dimensione della profondità.

La stessa cosa non succede guardando i quadratini neri. Guardando questi vediamo quelli verdi e azzurri in diplopia omonima. Muovendoci nel piano dei neri non vediamo nessuna linea immaginaria che unisce i quadratini neri, verdi e azzurri. Ciò significa che questi non hanno una collocazione precisa in profondità. Ciò mi fa concludere che la diplopia omonima dà luogo ad una stereopsi di secondo livello, ad una profondità grossolana che invita ad andare oltre.

sperimentiamo lo spazio binoculare

1) la stereografia
Tutti noi disponiamo di due occhi e perciò di due tipi di visione. Quando chiudiamo un occhio abbiamo la visione monoculare, caratterizzata da una visione in prospettiva, mentre normalmente, usando due occhi, abbiamo la visione binoculare, la quale è caratterizzata dall’area di Panum. Nel nostro vivere quotidiano non percepiamo la differenza tra le due, se non per il fatto che con due occhi si vede meglio che con uno. Del resto degli indici di profondità in grado di creare la stereopsi ci sono anche nella visione monoculare, per esempio il movimento, la sovrapposizione, l’intensità del chiaroscuro, eccetera. Ho inventato questi esperimenti allo scopo di mettere in evidenza come percepiamo lo spazio nella visione binoculare. Per fare ciò ho ritenuto opportuno utilizzare un laboratorio che non costa nulla, in modo da creare delle situazioni semplificate, senza il rumore del chiaroscuro, dell’atmosfera, del movimento e di tutto ciò che ci nasconde come in effetti percepiamo lo spazio binoculare. Questo laboratorio sfrutta la diplopia crociata per creare la visione binoculare da un semplice disegno e si chiama stereografia. Perciò prima di tutto cerchiamo di capire come funziona la stereografia. Quando i nostri occhi convergono su un oggetto, lo vediamo nitido, mentre un oggetto più vicino o più lontano da esso lo vediamo doppio, due volte, si dice in diplopia. Ciò è mostrato dal disegno seguente nella raffigurazione a sinistra: Os è l’occhio sinistro, Od è l’occhio destro, A è il punto di vergenza, B è un punto in diplopia. In basso il disegno mostra la sovrapposizione delle due prospettive in cui Bd rappresenta il punto B visto dall’occhio destro e si trova a sinistra del punto principale, Bs rappresenta il punto B visto dall’occhio sinistro e si trova a destra del punto principale. Questa diplopia si chiama crociata. Abbiamo due punti, A e B, però ne vediamo tre: A visto dai due occhi, Bd visto solo dall’occhio destro e Bs visto solo dall’occhio sonistro. Questo primo disegno è servito a spiegare cos’è la diplopia, adesso prendiamo in considerazione la raffigurazione di destra per spiegare cos’è la stereografia. Su un piano abbiamo due punti uguali come forma e colore: il punto B e il punto C. Adesso uniamo questi punti con delle rette che rappresentano i raggi visuali con Os e Od, che rappresentano gli occhi, ottenendo i segmenti OsB e OsC da un lato e OdB e OdC dall’altro lato. Prolunghiamo i segmenti OsB e OdC che si incontrano nel punto B+C, il quale rappresenta un punto virtuale che si trova oltre il piano di fondo. Guardando il punto B o il punto C vediamo due punti, ma se con lo sguardo andiamo altre il piano di fondo, cercando di guardare lontano, vediamo che il punto B e il punto C cominciano a muoversi per fare posto al punto B+C, il quale è la fusione del punto B e del punto C perché visto da entrambi gli occhi e per questo motivo è stereografico, cioè viene visto nello spazio. La diplopia del punto B e la diplopia del punto C ci fanno vedere quattro punti, ma in questa particolare situazione due punti combaciano e perciò vediamo tre punti. Nella prospettiva sotto il disegno ho segnato con B l’immagine di B vista solo dall’occhio destro e si trova a sinistra del punto principale, perché è in diplopia crociata; ho segnato con C l’immagine di C vista solo dall’occhio sinistro e si trova a destra del punto principale per lo stesso motivo di B. Ho segnato con B+C l’immagine del punto virtuale B+C, fusione di una immagine del punto B e di una del punto C. Questo è il funzionamento di una stereografia.













2) esercizi di riscaldamento
Per vedere una stereografia con questo sistema occorre un poco di concentrazione e una preparazione, perché bisogna imparare a guardare oltre il foglio da disegno. Adesso guardiamo il seguente disegno composto da due linee. L’esercitazione riesce quando ne vedrete tre affiancate. Cominciate prima con le linee di sinistra. Dopo provate con le linee di destra, che richiedono maggiore concentrazione.

3) Confrontiamo lo spazio monoculare e quello binoculare

Sotto abbiamo due prospettive lineari eseguite in riferimento a due punti di vista vicini, come se fossero gli occhi che guardano lo stesso punto. Fatte le prospettive ho invertito l’ordine orizzontale, portando la destra alla sinistra, per la diplopia crociata.

Il riquadro di ogni prospettiva deve essere al massimo 6,5 cm, più o meno la distanza degli occhi. Bisogna vederle cercando di guardare oltre il foglio, con lo sguardo perso nel vuoto, rilassato. Se riuscite a fare ciò vedrete le due prospettive muoversi, allontanarsi per fare posto ad un terzo riquadro nel mezzo. Cercate di far combaciare lo spigolo più vicino a voi del parallelepipedo rosso. Fatto ciò, potete muovere lo sguardo guardando gli altri partocolari delle tre prospettive.

La prospettiva che vedete sulla sinistra è vista solo dall’occhio destro e non c’è effetto stereoscopico. La prospettiva che vedete sulla destra è vista solo dall’occhio sinistro, anche in questo caso l’immagine è piatta. La prospettiva che vedete al centro è stereoscopica perché vista da entrambi gli occhi. Stereoscopica significa che vedete la profondità, che vedete la strada scivolare davanti a voi.

Con questo sistema abbiamo davanti ai nostri occhi contemporaneamente la visione monoculare, rappresentata dalle due prospettive lineari agli estremi, e la prospettiva binoculare, rappresentata dalla prospettiva centrale stereoscopica.

4) il punto di vergenza

Il punto di vergenza, di convergenza degli occhi, è di fondamentale importanza come indice di profondità per il nostro cervello, da solo crea stereopsi.

Nei nostri esperimenti privileggeremo due punti di vergenza: uno è il punto di fuga della strada, l’altro è lo spigolo più vicino a noi del solido, quello più lungo. La distanza tra i due spigoli è inferiore di circa un centimetro alla distanza dei due punti di fuga. Questo significa che quando il punto di vergenza è lo spigolo, la convergenza degli occhi è maggiore che quando il punto di vergenza è il punto di fuga, avendo come riferimento l’angolo retto della visione lontana. Per convincersi di ciò basta guardare nel primo disegno l’immagine di sinistra. In essa il punto B è più vicino del punto A e perciò l’angolo dei raggi visuali si discosta di più dall’angolo retto, che quando si guarda il punto A, che è più lontano. Questo significa che, da un lato, cambiando il punto di vergenza muta la convergenza degli occhi, dall’altro lato, che l’immagine stereografica simula alla perfezione una situazione reale.

5) la fusione

Quando il punto di vergenza è lo spigolo del solido, i muscoli della convergenza degli occhi fanno in modo che i due spigoli coincidono; lo stesso avviene quando il punto di vergenza è il punto di fuga della strada, cioè vengono sovrapposti i due punti di fuga. In entrambi i casi c’è una confusione di linee, come da disegno sotto:

Mentre se riguardiamo l’immagine stereografica questa confusione non c’è.

Per capire in effetti cosa succede semplifichiamo le due prospettive togliendo il solido e utilizzando colori diversi. Però prima dobbiamo richiamare la capacità del cervello di deformare la visione, al punto da farci vedere le linee rette come curve. Per vedere questo ci serviamo dell’illusione di Hering, detta anche illusione del ventaglio. Le due linee blu sono due rette parallele, come si può facilmente verificare.

Premesso questo osserviamo l’immagine stereoscopica che si crea osservando in modo opportuno le seguenti prospettive affiancate, scegliendo il punto di fuga come punto di vergenza. Queste prospettive sono state fatte apposta con colori diversi per rendere più chiaro il concetto di fusione.

L’immagine stereoscopica che si crea, avendo come punto di vergenza il punto di fuga, togliendo l’effetto tridimensionale, la vediamo più o meno così, come il seguente disegno.

Ciò che si nota è che il cervello, attraverso una illusione ottica del tipo di Hering, deforma le rette corrispondenti per farle combaciare, infatti vicino al punto di vergenza, il punto di fuga, le rette combaciano a due a due. Questo processo è detto “fusione”. Però bisogna anche osservare che questo riesce al cervello entro un certo grado, oltre il quale vince la diplopia. Per questo le rette da un certo punto in poi divergono.

6) la profondità binoculare

La parola “stereoscopia” significa vedere lo spazio, cioè la profondità. Nella visione binoculare la profondità non è infinita, arriva poco oltre il punto di vergenza. Infatti oltre l’area di Panum la fusione non avviene più perché la diplopia è elevata, oltre la capacità di fusione del cervello. Guardando l’immagine stereoscopica proposta sembra che c’è una profondità immensa, questo perché avete come punto di vergenza il punto di fuga della strada. Anche guardando il solido sembra che la profondità non cambia, perché gli occhi si muovono continuamente da un punto all’altro. Proviamo a fissare lo spigolo maggiore del solido muovendo lo sguardo, perché fermo non può stare, in punti diversi sempre dello spigolo suddetto, facendo attenzione, con la coda dell’occhio, al punto di fuga. La prospettiva che vediamo, tolto l’effetto stereo, è la seguente:

Vediamo due punti di fuga, effetto dovuto alla diplopia, ognuno dei quali è visto con un occhio, per cui manca l’effetto stereo, manca quella profondità che si avverte quando lo sguardo va avanti e indietro. Ciò che vediamo è un solido che risalta sopra un fondo piatto, quasi fosse un alto rilievo.

7) acuità visiva

Oltre la fusione interviene un altro motivo a ripulire la sovrapposizione delle due prospettive da parte del cervello: l’acuità visiva. Questa è dovuta alla struttura della retina, che si articola nella visione colorata e particolareggiata dovuta ai coni, e nella visione della luminosità e del movimento dovuta ai bastoncelli. Ciò significa che noi vediamo bene solo al centro del campo visivo, per un’ampiezza di appena un grado, che corrisponde all’ampiezza della fovea. Praticamente alla distanza di quaranta centimetri, che è più o meno la distanza dal monitor, l’area che corrisponde alla fovea ha un diametro poco più di mezzo centimetro. Parlando della profondità binoculare, abbiamo detto che guardando lo spigolo del solido, va in diplopia il punto di fuga della strada. Corrispondentemente guardando il punto di fuga va in diplopia il solido. Però non ci accorgiamo di questo perché esso è distante dal punto di fuga e cade nella visione periferica. Però fissando il punto di fuga, con la coda dell’occhio, si intravede la diplopia del solido, come prima avevamo notato la diplopia del punto di fuga. Il disegno seguente mostra la diplopia nei due casi.

Sul significato della parola arte

A mio parere, l’ottocento e il novecento hanno snaturato il significato della parola arte ingiustificatamente, pur premettendo che il mio è un discorso da pittore, non sono né un linguista, né un filosofo. Parlo perché vedo tanti ragazzi che scelgono gli studi artistici in quanto portati al disegno e alla pittura e alla fine degli studi non disegnano e nemmeno dipingono. Imparano a fare provocazione.
Studiando la storia dell’arte si capisce che il temine “arte” significa “ordine”, infatti si dice “arte dorica” oppure “ordine dorico”; si dice “ordine corinzio” per dire “arte corinzia”. Oggi alla parola “ordine” si preferisce la parola “stile”, questo da quando nella seconda metà del milleottocento si voleva che l’arte fosse come la musica, allora, la parola “stile” che era nata per designare l’ordine della scrittura, che si era evoluta designando l’ordine dei suoni, era passata a designare l’ordine delle forme. Perciò la parola “ordine” e la parola “stile” hanno lo stesso significato. Per ordine si intende la geometria spaziale di un oggetto, cioè la composizione, la disposizione, il carattere, l’equilibrio, la simmetria, la linea, eccetera. Però il lavoro dello storico dell’arte non si ferma qui, egli studiando i costumi, la filosofia, la storia di un popolo, lega quel determinato stile a tutto quel mondo spirituale che gli sta dietro e ne spiega così la necessità. Quindi “arte” sta per “ordine più significato”.
Al tempo delle corporazioni si discuteva se era giusto che i pittori facessero parte delle arti meccaniche, perché, facendo parte della corporazione dei tintori di lana, erano poco pagati e non erano rappresentati nel governo della Firenze di fine trecento. Questo portò alla rivolta dei Ciompi, con la quale i pittori ebbero una rappresentanza nel governo della città e fu riconosciuto loro che il lavoro del pittore era un lavoro intellettuale, perché dovevano conoscere la prospettiva e i testi sacri. La conseguenza di ciò portò il Ghiberti a scrivere un libro di storia dell’arte in cui, per la prima volta nella storia, stavano insieme pittura, scultura e architettura. I secoli seguenti accettarono questo insieme di discipline come rappresentative dell’insieme arte. Con questo voglio dire che la storia dell’arte come storia di pittura, scultura e architettura ha avuto un inizio ed era giusto che avesse una fine. Ciò che mi fa pensare non è questo, è ciò che è avvenuto a metà del millesettecento, epoca della manifattura. L’enciclopedia è la massima espressione di questo periodo, dove, attraverso i suoi autori, venivano esposte le due tesi dell’arte: d’Alembert sosteneva che l’arte è un dono di natura, che non si insegna (è strano che si sia creduto possibile sostituire con regole un talento così raro: sarebbe come voler ridurre il genio ad una precettistica) mentre Diderot poneva l’accento sulla scuola e sull’esperienza (se l’oggetto va eseguito, l’insieme e la disposizione tecnica delle norme secondo le quali va eseguito si dicono arte). Forse il mondo è fatto in modo tale che il massimo coincide con l’inizio del minimo, perché nello stesso tempo Baumgarten utilizzava la parola “estetica”, con la quale cambiò il significato della parola “arte”, che non era più “ordine prodotto con le mani”, bensì, “ordine che colpisce la nostra sensibilità”, cioè “ordine bello”. Tutto questo rietrava nell’atteggiamento preromantico che, nel tentativo di costruire dei significati fondati sulle nostre reazioni psicologiche, cambiò il significato di alcune parole. Per esempio il contrario di bello non era più brutto, perché brutto significava meno bello, ma sublime, in quanto il bello dà un senso di sicurezza, mentre il sublime, che indica il passaggio dallo stato solido a quello aeriforme, era lo scioglimento del nostro animo provocato da un evento inaspettato e terribile. Ora, se prendiamo un dizionario filosofico e cerchiamo la parola “arte” ci rimanda alla parola “estetica”, come se “arte” ed “estetica” avessero lo stesso significato. Questo sarebbe accettabile se l’estetica fosse la “scienza dell’arte”, ma l’estetica è definita, in filosofia, come la “scienza del bello e dell’arte”, definizione che porta a far coincidere “arte” e “bello”. La strada verso la distruzione della parola “arte” era aperta, perché tutto ciò portò a far diventare relativo, come è relativo il concetto di bello, il concetto di arte. Infatti gli etnografi, nel lavoro di indagine sui popoli rimasti fuori dal cerchio della civiltà, hanno preso gli oggetti prodotti da questi ed hanno chiesto quale fosse bello per loro. Ciò portò Marcel Mauss nel 1947 a scrivere che “un oggetto d’arte per definizione è un oggetto riconosciuto came tale da un gruppo”; il relativismo è totale. Praticamente Mauss dice che niente distingue l’oggetto d’arte dagli altri se non il fatto di essere stato scelto. Questo è vero per la religione perché qualunque oggetto può rappresentare il divino, in quanto ciò che si cerca non è un oggetto, ma un simbolo. Ciò che io non capisco è perché se studiamo l’arte greca accettiamo nell’insieme arte tutti gli oggetti trovati, descrivendoli attraverso lo stile e studiando ciò che è rimasto delle scritture greche per ricostruire, nel limite del possibile, il mondo spirituale dei greci, cercando di vedere la nacessità che ha prodotto questi oggetti. Siamo sicuri che, se fosse possibile, chiedendo al contadino greco di allora, quale di questi oggetti fosse bello per lui, avesse risposto il Partenone? O chiedendo allo schiavo egiziano, che avrebbe risposto la piramide di Cheope?

Lucia Giugno sulla pittura binoculare

Il lavoro di Nino Venezia è improntato a capire i meccanismi della visione, i quali operano nella nostra più assoluta inconsapevolezza, con l'antico strumento della pittura. Anche gli argomenti di cui parla sono vecchi, ci riportano ai tempi in cui l'arte era ancora un tema celeste: la prospettiva, la macchia, il disegno; però vale la pena ascoltarlo per l'interesse scientifico con cui affronta l'argomento, che proprio per questo diventa attuale. Per entrare nel personaggio bisogna sapere che è molto legato alla manualità, non nel senso manierista, che la mano esprime uno stile personale, nemmeno Freudiano, che attraverso il gesto della mano si liberano pulsioni interne, ma nel senso che vede la mano e l'arte legate da un legame indissolubile, al punto tale che per lui ciò che non è fatto dalle mani non è arte. Questa convinzione la giustifica dicendo che le parole “arte” e “arto” hanno la stessa radice, ed è una delle parola più antiche, di quando gli uomini usavano poche parole ed erano tutte necessarie, non come oggi che la parola arte significa tutto e niente. La parola arte, in sanscritto, significava ordine, disposizione, e l'arto era l'ordinatore, lo strumento con cui l'uomo mette ordine. In questo senso l'arte e la mano sono legate insieme. C'è di più, per lui la parola ordine è diventata una filosofia, mi ripete sempre che la creazione non si è fermata al settimo giorno, perché la creazione di nuovi ordini crea nuovi significati, senza che cambi niente nell'universo da un punto di vista fisico. Questo spiega il suo accanimento nel campo della pittura, dove da un punto di vista tecnico non l'ho visto mai in difficoltà, lavora con la stessa disinvoltura ad impasto come a velature, con gli inchiostri come con i colori ad olio, a matita come a carboncino. Perciò il discorso non è se riesce ad esprimere le proprie idee attraverso la pittura, ma se attraverso essa riesce a stimolare la nostra curiosità, molla di ogni interesse. Quando mi sono trovata davanti le sue opere ho capito subito ciò che era evidente, che il punto centrale della tela era molto curato, rifinito, al contrario della parte periferica della tela dove tutte le forme erano sfocate. Errore, mi disse, non sono sfocate, le macchie sono semplicemente più grandi, per cui saltano i particolari. Poi ho capito, quando mi invitò ad avvicinarmi al quadro e a guardare il centro della tela, che la struttura dell'occhio, con al centro i coni ed in periferia i bastoncelli, corrisponde alla composizione della tela. Ero tentata di spostare lo sguardo nella periferia della tela, non lo feci perché mi piaceva fare attenzione a quelle larghe macchie cercando di capire la visione con i bastoncelli. Fu con questa visione che quelle macchie mi sembravano perfette, addirittura avevo la sensazione di avere davanti a me una pittura tridimensionale. Questa esperienza ha fatto scattare in me la molla della curiosità, così mi sono avvicinata alla parte intellettuale della pittura binoculare di Nino. Di questa mi è piaciuto il riferimento all'attenzione. Se dividiamo la visione degli occhi con uno specchio, in modo che con un occhio guardiamo davanti e con l'altro di lato, il nostro cervello sovrappone le due prospettive, però non potendo arrivare ad una visione unica, sopprime le parti di prospettiva che non interessano, quelle parti che, per scopi vitali, non meritano la nostra attenzione. Questo meccanismo agisce nell'uomo nascondendo in parte la diplopia della visione binoculare; è questo meccanismo che che fa la differenza tra la fotografia, dove tutto è presente, e la visione umana che è fatta di attenzioni e soppressioni. Mi è piaciuta la sua nuova teoria del colore fondata sulla visione umana, perché va oltre gli scopi fotografici del fotoritocco. Il colore è intenso solo al centro del quadro e poco saturo in periferia, in parallelo alla struttura della retina che permette la visione colorata solo con la fovea, dove ci sono i coni abilitati alla visione a colori. Un'attenzione particolare merita la geometria dello spazio fondata sull'oroptero, il cerchio comune a due prospettive che hanno un punto di vergenza, cioè di due prospettive che guardano lo stesso oggetto. Questo addirittura dovrebbe farci cambiare modo di esprimerci in riferimento alla distinzione tra soggetto e piano di fondo, dovremmo dire cerchio di fondo, perché la visione umana è fatta di cerchi e non di piani. L'oroptero è quel cerchio che passa dall'oggetto guardato a dai nostri occhi ed è soprattutto l'area dove avviene la fusione, detta area di Panum, un altro meccanismo che due macchine fotografiche non possono avere, perché è una prerogativa del nostro meraviglioso cervello. In quest'area la visione è tridimensionale e la pittura di Nino non lo è. Egli dipinge gli oggetti che si trovano nell'oroptero con la prospettiva artificiale, come una macchina fotografica per intenderci, usando tutti i trucchi che un pittore conosce per dare il senso del rilievo. Questo scarto tra la sua pittura e la visione binoculare non è così rilevante in quanto interviene un altro fattore dovuto alla struttura della retina: l'acuità visiva. Questa ci fa vedere bene solo un punto che corrisponde al centro della fovea, poi, allontanandoci da esso, vediamo macchie sempre più grandi dove i particolari si perdono. Perciò la pittura di Nino è fatta di un centro ricco di particolari e dal colore intenso, e di una periferia con larghe macchie dai confini non sempre tangibili, dove ogni riferimento prospettico si perde. Questo vuol dire che guardando un quadro binoculare al centro, in modo che copra quasi tutto il campo visivo, si ha una visione molto vicina all'esperienza reale. Questa è una constatazione personale che il lettore, volendo, può provare e che, a mio parere, giustifica il nome “binoculare” con cui Nino chiama la sua pittura. Un'ultima cosa mi preme rilevare: la presenza del disegno nella parte centrale. Nella storia dell'arte, quando si affronta lo studio dei macchiaioli, si insegna che il disegno non esiste, infatti se guardiamo una fotografia non c'è disegno, ci sono macchie e sfumature. Lui mi disse che si riferisce al meccanismo on-off delle cellule ganglionari, che reagiscono solo ne caso in cui tra il centro e la periferia c'è un contrasto di luce. Ciò significa che se una cellula della retina è totalmente alla luce, o totalmente al buio, non reagisce. Questo meccanismo mette in risalto i contorni, il disegno è un contorno. L'unico rimprovero, detto alla buona, è che lui parla troppo del suo lavoro, quasi non lascia niente all'immaginazione dello spettatore; è che lui ragiona troppo sulla pittura, che parla alla nostra sensibilità. Però bisogna riconoscere che sensibilità e ragione sono gli elementi di cui ogni individuo è dotato e non si possono dividere. L'estetica ha voluto dividere le due sfere attribuendo l'arte a quella della sensibilità, come se questo fosse possibile. Quindi ben vengano i pittori razionali come Nino Venezia, di cui di una cosa possiamo essere sicuri, conosce il suo mestiere maledetto.

Niscemi, 10 aprile 2008, Lucia Giugno

seguono le ultime opere

Oroptero

Consideriamo la prospettiva in cui i punti di vista sono due, per simulare la prospettiva vista da due occhi, per questo motivo questa prospettiva si chiama binoculare. Per semplicità supporremo che il punto guardato sia alla stessa altezza dei due punti di vista in modo tale che questi tre punti formino un triangolo orizzontale. Questa semplificazione non è un limite, nella misura in cui attraverso una rotazione del sistema di riferimento, ci si può sempre riportare alla situazione supposta. In questa condizione le due prospettive hanno in comune il sistema di riferimento: la linea di terra, la linea di orizzonte e il punto principale. La linea di terra, che rappresenta il piano di appoggio dei piedi, e la linea di orizzonte, che rappresenta l’altezza degli occhi dell’osservatore, perché sono uguali per entrambi gli occhi. Il punto principale perché ha la stessa funzione della fovea nell’occhio. Come il punto principale è il centro del cerchio ottico sul quadro, così la fovea è il centro della retina. I due punti principali coincidono in quanto le due prospettive vengono sovrapposte nella corteccia visiva con un processo di integrazione.

Le due prospettive non sono uguali, anzi proprio la disuguaglianza orizzontale serve al sistema percettivo per creare la stereopsi, e questa disuguaglianza orizzontale si chiama disparità. Da un punto di vista geometrico le due prospettive, proprio con la loro diversità, danno luogo alla prospettiva binoculare, che ha un funzionamento diverso dalle prospettive di origine. Nella prospettiva lineare bisogna stare attenti al parallelismo delle rette in quanto rette parallele convergono allo stesso punto di fuga. Nella prospettiva binoculare bisogna stare attenti all’oroptero, il cerchio che le due prospettive hanno in comune. In questa prospettiva ogni retta ha due punti di fuga e due intersezioni col quadro binoculare, questo significa che ogni punto viene rappresentato due volte. Però esiste un luogo geometrico in cui questo non accade, questo è l’oroptero. Nella rappresentazione ortogonale del piano orizzontale fissiamo a piacere tre punti non allineati, due vicini che rappresentano gli occhi, uno più lontano che rappresenta il punto guardato. Essi formano un triangolo.

Poi tagliamo il lato destro del triangolo con una retta perpendicolare ad esso ad una distanza a piacere dal vertice che il lato stesso ha in comune con la base. In questo modo abbiamo fissato gli estremi per la prima prospettiva, infatti abbiamo costruito un punto di vista, un punto oggetto da guardare e, l'ultima retta disegnata, il quadro. Operiamo nello stesso modo sul lato sinistro del triangolo con le stesse misure.

Adesso prendiamo in considerazione la prospettiva di destra e stacchiamo un punto ad una distanza a piacere dal punto principale sulla retta che rappresenta il quadro. Uniamo questo punto col punto principale e prolunghiamolo dalla parte opposta, oltre il quadro. Questo rappresenta un raggio visuale. Operiamo nello stesso modo e con lo stesso fine sulla prospettiva di sinistra ottenendo un altro raggio visuale che abbia la stessa distanza e stesso verso dal punto principale dell'altra prospettiva. I due raggi visuali così ottenuti si incontrano in un punto e lo chiamiamo D. La prospettiva binoculare del punto D è rappresentata da un solo punto, perché nella sovrapposizione delle due prospettive come combaciano i due punti principali così combaciano le due rappresentazioni del punto D.

Se adesso facciamo la stessa cosa trovando altri punti ci accorgiamo che questa è la costruzione del cerchio.

Ciò significa che quando guardiamo un oggetto, tutti gli oggetti che si trovano sulla circonferenza che passa dall'oggetto osservato e dai nostri occhi li vediamo come se fossero visti da una sola prospettiva, perché nei punti dell'oroptero le due prospettive combaciano. Nello stesso tempo gli oggetti che si trovano dentro e fuori dal cerchio si sdoppiano. Per verificare questo basta mettere un dito più vicino ed uno più lontano, quando si guarda il dito vicino si sdoppia quello lontano e viceversa. La curva dell’oroptero non è influenzata dalla direzione dello sguardo, a destra, a sinistra o di fronte perché per tre punti passa una sola circonferenza. Non è nemmeno influenzata dal tipo di prospettiva, piana o sferica, perché tra i punti del quadro piano e i punti del quadro sferico c'è una corrispondenza biunivoca, cioè ad ogni punto della sfera corrisponde un punto sul piano. Dipende soltanto dalla posizione dell'oggetto osservato e degli occhi.

L’oroptero non è una superficie cilindrica, infatti se facciamo la prospettiva della circonferenza dell’oroptero sul piano orizzontale si hanno due curve, una per ogni occhio. Le due rappresentazioni del punto A, in riferimento al disegno sotto, coincidono sulla linea di orizzonte. Sul quadro, l’oroptero è un segmento che va dal punto B al punto C sulla linea di orizzonte.

La realtà è molto più complessa, abbiamo oggetti in tre dimensioni, più o meno vicini e in tutte le direzioni, infatti anche il discorso sull’oroptero è molto più complesso, non si ferma qui. Continuiamo osservando che gli angoli che i punti dell’oroptero formano con i due punti di vista sono tutti uguali.

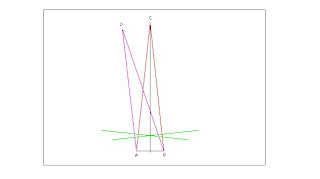
Riferendoci alla figura seguente l’angolo in C è uguale all’angolo in un punto qualunque dell’oroptero, per esempio D. Infatti dall’uguaglianza dei triangoli APF e BPE si deduce che la somma degli angoli alla base dei due triangoli, ABC e ABD è uguale.

La visione non è fatta solo dei punti dell’oroptero, ci sono punti dentro, cioè più vicini, e punti fuori l’oroptero, più lontani. Quando il punto è dentro l’oroptero, l’angolo al vertice è maggiore di quello del punto di vergenza, quando è fuori è minore. Riferendoci alla figura seguente, l’angolo in D è maggiore dell’angolo in C, mentre l’angolo in E è minore.

Nella figura seguente si è messo in evidenza, del disegno precedente, la parte riguardante i due punti di vista e i due punti principali, chiamati entrambi P. Il triangolo ABD è interno al triangolo ABC e i lati AD e BD intersecano il quadro nei punti F, interni al triangolo ABC. Non dimenticando che C è il punto di vergenza, il tratto FP si chiama disparità crociata perché è interna al triangolo ABC. Dalla parte opposta abbiamo messo in evidenza il tratto GP, il quale è esterno al triangolo ABC, conseguenza del fatto che il triangolo ABE è esterno al triangolo ABC, per questo motivo si chiama disparità non crociata.

A questo punto ciò che è importante notare è che la misura della disparità crociata è direttamente proporzionale agli angoli che si formano sui rispettivi oropteri, cioè più grande è la disparità crociata più grande è l’angolo al vertice del triangolo che il punto oggetto forma con la base fatta dai punti di vista. Al contrario, la misura della disparità non crociata è inversamente proporzionale agli angoli degli oropteri esterni, cioè più grande è la disparità non crociata più piccolo è l’angolo all’oroptero. Siccome ad ogni angolo corrisponde un oroptero, la mente sa sempre a quale oroptero appartiene un punto.

Se adesso noi sovrapponiamo le due prospettive facendo coincidere la linea di terra con la linea di terra, la linea di orizzonte con la linea di orizzonte e i due punti principali, il punto D, essendo in disparità crociata, e il punto E, essendo in disparità non crociata, sul quadro vengono rappresentati due volte sulla linea di orizzonte, in quanto non appartengono all’oroptero del punto di vergenza, inoltre i punti presi in considerazione, appartengono tutti al piano determinato dai due punti di vista e il punto guardato. Ciò significa che se il nostro cervello sovrapponesse semplicemente le due prospettive dei due occhi quando guardiamo un oggetto, di esso dovremmo vedere chiaramente solo un punto, in quanto qualunque oggetto, avendo tre dimensioni, ha punti in oropteri diversi, che avrebbero due immagini. Invece il cervello, tramite la disparità crociata e non, riferisce ogni punto dello spazio ad un oroptero diverso. Se la disparità è crociata, le due immagini del punto vengono fuse, vediamo un solo punto però più vicino rispetto al punto di vergenza, il punto guardato. La stessa cosa vale per la disparità non crociata, le due immagini vengono fuse, cioè ne vediamo una sola però più lontana rispetto al punto di vergenza. Questo miracolo operato dal cervello si chiama fusione. Essa è la capacità del cervello di costruire una mappa tridimensionale dello spazio che ci circonda. In altre parole noi non vediamo in prospettiva il mondo che ci circonda, lo vediamo in tre dimensioni; non vediamo un mondo in prospettiva, cioè piatto con degli indici di profondità, bensì lo vediamo in profondità.

A questo punto il discorso si è semplificato in quanto tutto ciò che si è detto è servito a chiarire che noi vediamo in tre dimensioni. Però il cervello non riesce ad operare la fusione per tutti i punti dello spazio, opera la fusione solo per i punti oggetto che si trovano in prossimità dell’oroptero, è come se esso avesse uno spessore, un’area che si chiama area di Panum. Dagli esperimenti fatti risulta che essa è più stretta al centro e più larga ai lati, come mostra il disegno sotto.

Per concludere, nella prospettiva binoculare si possono distinguere tre zone: quella principale a cui appartiene l’oggetto guardato che è la zona di punti singoli visti nelle tre dimensioni, che è più stretta al centro e più larga ai lati; la zona di disparità crociata, a cui appartengono gli oggetti più vicini del punto di vergenza, con due immagini distinte per ogni oggetto, in cui l’immagine di destra rappresenta ciò che vede l’occhio destro; infine la zona della disparità non crociata, a cui appartengono gli oggetti più lontani del punto di vergenza, con due immagini distinte per ogni oggetto, in cui l’immagine di destra rappresenta ciò che vede l’occhio sinistro